Science is all about making mistakes and checking your work. Today... was a science day...
I had been listening to this video from Fermilab:
Which got me to wondering if I had been doing my math right.
Unable to remember my original sources, I googled for "travel constant acceleration" and found that basically everyone on the internet pointed to "The Relativistic Rocket" link http://math.ucr.edu/home/baez/physics/Relativity/SR/Rocket/rocket.html.
Using that page I re-jiggered my formulas into something I could plot stepwise in an excel sheet. And even better, check my work by using different formulations.
I uncovered several goofs in my original math. Travel time was fraction what my existing formulas were predicting. (7 years not 18 years, proper time.)
I thought I was off the hook, with perhaps a small plot-rewrite when I decided to read further down the "the Relativistic Rocket" and the section on Fuel usage. Let's just say that my original trip to 18 Scorpii 45.5 light years away would have required 2400 times more fuel than the ship weighed empty. And it doesn't matter (heh) what sort of propulsion system I was using. Even some sort of matter/anti-matter smasher would require that much mass (ok technically half that mass, and half of that anti-mass) to get the vessel up to the .999996 c required to make the trip.
Well... whoops.
So I got to thinking. Is constantly accelerating (and then decelerating) necessary? Let us say the the vessel accelerated up to some fraction of C then stopped. We then let it coast, perhaps losing a little speed due to drag. (There are still trace bits of gas and dust in interstellar space.) When the vessel is a (calculated) distance away from the remote system, we turn it around, and decelerate.
But what speed? Too fast and we require an amount of material that I can't (at least in good conscience explain away. Too slow and I'll introduce improbably to solve logistics issues about keeping spare parts in stock and the colonists from going completely crazy.
Going back to my engineering school days, I decided it was best to make a few graphs and try to see of there was a geometrical solution to my problem.
My first graph charts the total length of the trip. Which combines several factors:
- Accelleration is constant. A vessel takes a longer distance to reach a higher coasting speed. This distance cuts into the total distance spent coasting. Twice in fact, because we get to subtract this from the end. (We calculate proper time for accel/decel separately.)
- The closer the ship gets to the speed of light, the more time dilation shrinks the proper time on the vessel during the coast phase.
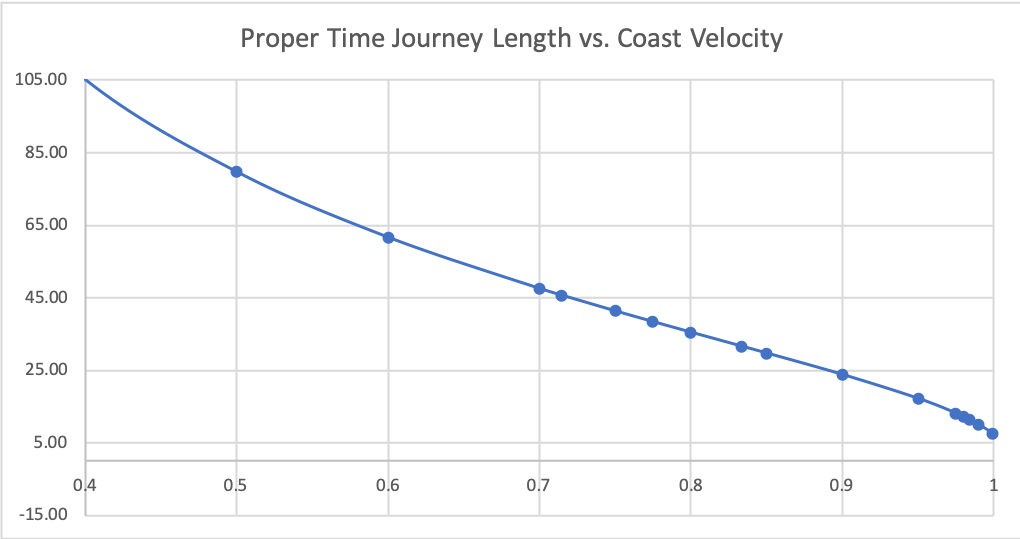
You'll see I threw out any speed below 0.4c. This is because we get exponentially larger travel times. For 0.1c, the ship takes 500 years to travel between the Sol and 18 Scorpii system. The best we can do it to accelerate halfway, and then immediately decelerate. For that we reach 0.99917c, and the trip takes 7.55 years. Basically the smaller the number on the Y axis, the better.
Next I graphed the fuel mass to payload mass required for the same data points I calculated for the first graph:
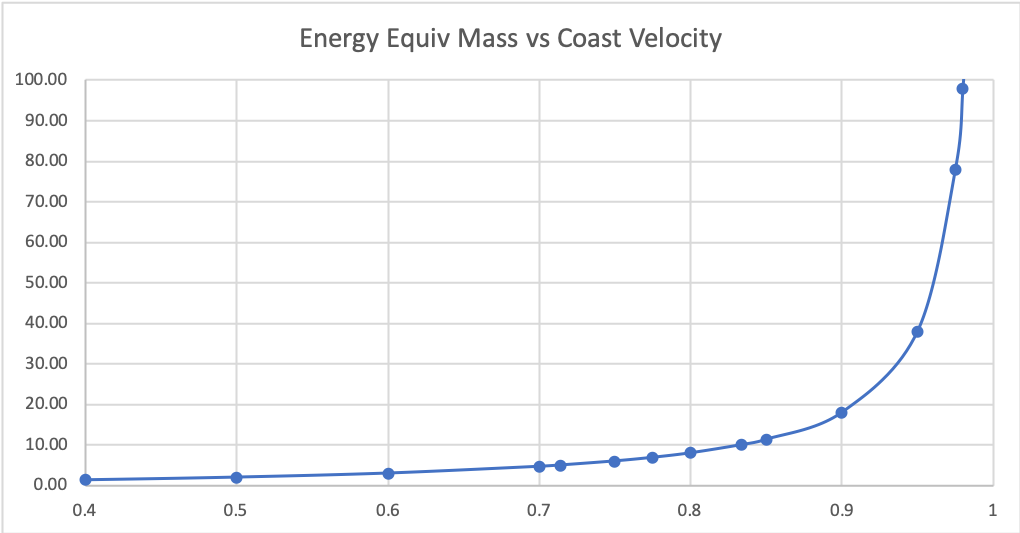
I clipped the Y axis at 100x the payload mass. Those values aren't interesting. Like the graph above, the smallest number on the Y axis, the better. The best is obviously 0.1c which only requires 0.22 vessel masses of fuel. The worst is our constant accel/decel which requires 2400.
My eye is immediately drawn to the 0.9c areas of the fuel usage chart. And if it helps, the two Y axes ended up (by a complete coincidence) in the same range. So here are both graphs laid on top of each other:

The blue line is fuel mass (in number of vessel masses), the orange line is travel time (in years, proper time). They cross pretty near that 0.9c mark.
So at 0.9c our ship has to somehow convert 18x its own mass into pure energy to get itself up to its cruising speed, and then to also have enough fuel to slow itself back down. And while 18x the ships mass seems like a lot, remember that this ship does not have to lift off from Earth. It is starting it's journey in the Oort cloud.
Let is say that all of my ship drawing so far are simply the "Interesting" parts of the ship. The living spaces. The engines. The power production facilities. You almost always see pictures of the space shuttle as the shuttle itself. Not booster rockets. Not massive fuel tank. Just the shuttle:

If I look online for a space shuttle toy, this is the most common thing I'll find:

Compare this to the entire SLS system:

And even if those parts were on a drawing, there is no way for an astronaut to access those cryogenic tanks or solid rocket boosters in flight. So, we can continue to leave it off.
For story telling purposes, ships like this work similar to the craft in Arthur C. Clarke's 2061: Odyssey Three. While the primary energy source is some form of fusion, that energy needs to be converted into something physical to move the spacecraft. In Clarke's book, the ships would keep massive tanks of ice. This ice would be heated to some fantastic temperature, accelerated to an incredible speed, and thrown out of a nozzle to provide thrust. (Or at least if I'm remembering the process correctly.) There is even a part of the book where a ship has to make an emergency top off of their fuel with comet water to have enough fuel for a rescue mission.
Assuming we have some sort of science fiction way to accelerate normal matter to the fraction of the speed of light, we don't really need to be picky about what that mass actually is. We just need a lot of it, a cheap way to gather it, and a non awkward way of storing it.
Given that we are probably energizing this material beyond the plasma state, any old-pulverized material will do. It just needs to be fine enough to be sucked up by some sort of giant vacuum cleaner. Ships based in on the Moon use Regloth. In the asteroid belt, it depends on whether asteroid dust is cheaper, or dirty ice, or some industrial byproduct of mining.
Vessels travelling between planets do NOT require massive amounts of reaction mass. A worst case trip from Earth to Neptune is 31.3 astronomical units. Hundreds of millions of kilometers, but only 0.0004954059 light years. Accelerating at 1g the entire time would be a total trip time of 16 days, and require only 0.02x the ship's own mass in reaction mass. The ship speed would only reach 0.0226c. That is still an incredible 6775989 m/s.
By comparison the space shuttle traveled at 7777.778 m/s in orbit. The New Horizons spacecraft reached 23000 m/s during its journey to Pluto. The fastest spacecraft of all time (so far) are the Helios probes. They reached 69444.44 m/s during their orbits of the Sun.
Getting back to the point at hand. Iliad missions do require a massive amount of reaction mass to make their journeys. Much, MUCH more than normal interplanetary trips. But, seeing as how travelling inside of the Solar system is comparatively cheap, whats to say the Iliads don't simply go to where there is a lot of pulverized mass that is available practically for the taking. (Plus fuel to get here.) Enter the Kuiper Belt and Oort Cloud.
Our vessel has mass of 6.11E+11 kg. To travel at 0.90c we would need to gather 1.099800e+13 kg of matter. Comets we have observed range from 1e13kg to 3e14kg in mass. Essentially, the ship could gather all of the material it needs for its trip from a single comet. And there are billions and billions of comets in the Oort cloud.
I am foreseeing that after construction these vessels would fly off to the Oort Cloud. They would seek out a comet of the right size and density. They would essentially suck all of the ice and dust from that comet into a giant tank. They wouldn't want to rely on the comet's structure to hold up under the 1g of gravity that the vessel's engines will subject it to. That tank of reaction mass would probably be spherical to minimize the amount of material required to build it. It would have some sort of massive steel structure that would connect it to the Iliad, holding up the comet's mass against the force of gravity produced by the ship's engines. (Not feeling creative enough to build that structure, let's make it a happy cloud.)
While that tank looks massive, remember that the material inside is only a little more dense than packed snow. The size is mainly dealing with the bulk. On the whole, heavy, yes. But nothing that a sufficiently built framework of steel couldn't hold together. Think of how little steel is needed to hold up a water tank in full Earth's gravity:

Which brings to mind a thought I had back when I was putting the block-3 design together. Namely that they wouldn't accelerate all of the way up to 1.0 g. They would instead use 0.8g to save on wear and tear. And in this case, it would also mean that they could skimp on steel structure. In fact, the slower the ship accelerates the less structure they actually need to hold up the tank.
Changing the rate of accelleration doesn't actually change much with our relativistic math. Dropping the accelleration from 1.0g to 0.8g adds about 1 year onto the journey (in proper time).
This mass in the front of the vessel also takes care of another detail I was glossing over. Something to cushion high-speed "interactions" with interstellar material. A micrometeorite now has a hell of a lot of material to drill through before it reaches the ship itself.
Holding that much mass on top of the vessel seems like it's going to require some heroic structure. Here is another design the fits the reaction mass around the ship, especially around the docking ring where she is strongest:
Another important thing to consider is we don't need the entire tank for the entire trip. The deceleration phase only requires 20% of the mass of the acceleration phase. It's complicated rocket math, but what is driving our equations to such ludicrous numbers is that it takes more than a kilogram to drive a kilogram... for the entire burn time. Cut the burn time in half, and you need a fraction of the reaction mass.
This design has the accelleration reaction mass in a discardable torus, with 20% of the reaction mass set aside in a separate spherical tank:
Depending on the construction technique, it may actually be more cost efficient to divide the fuel into smaller units, and then stack the rings of fuel:
Ok, well enough of that. I'm satisfied that with just a tiny bit of exposition and a minimum of explanation I can account for the biggest objection a decent physicist would have to this endeavor. They can probably buy some made up drive that can accelerate volumes of matter to near the speed of light. They can't hand wave the sheer amount of mass required to get something up to near light speed.